題敘

Link

給定一棵 $N$ 個點的樹， $M$ 筆查詢兩個點 $u,v$， 所有加一條邊（允許重邊）讓 $u$、$v$ 都在環裡的情況， 環長度的期望值是多少？

$1 \leq M, N \leq 10^5$

提示

Hint 1

思考簡單一點的狀況：如果問的是方法數要怎麼算出來？
有辦法在多好的複雜度？
　

Hint 2

思考完簡單的計算之後，要怎麼利用期望值就快速地計算出來？
　

Hint 3

總共需要對每個節點維護什麼東西？

　

想法

把情況看簡單一點，總共有兩個狀況：

Case 1

• 兩個點沒有間接祖先或小孩的關係

這樣問題很簡單，邊必須要連接兩個點的子樹， 利用樹 DP 的方式可以對每個子樹預處理子樹以下的期望值， 令 $k$ 是他們的最近共同祖先， $size[p]$ 是 $p$ 子樹的大小，$dp[p]$ 是 $p$ 子樹所有點到根的距離總和，$dis[p]$ 是 $p$ 到根的距離， 然後答案就是 $\frac{dp[u]}{size[u]} + \frac{dp[v]}{size[v]} - dis[k]\times 2 + 1$。

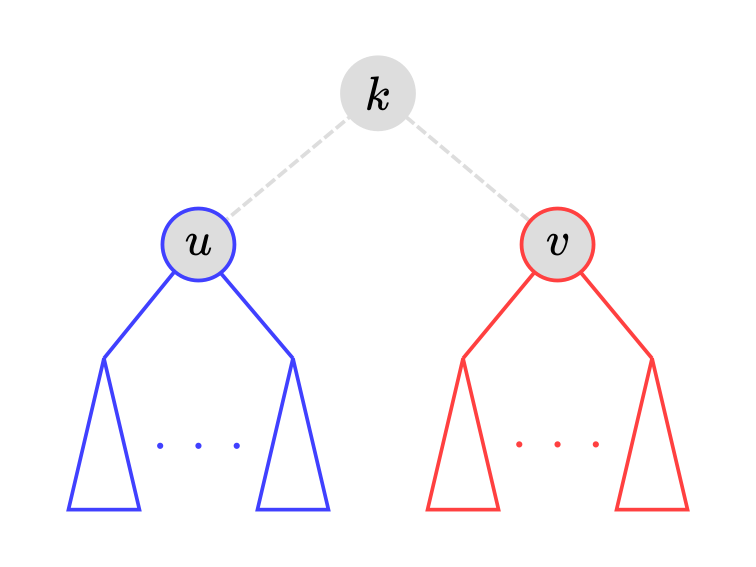
Case 2

• 兩個點有間接祖先或小孩的關係

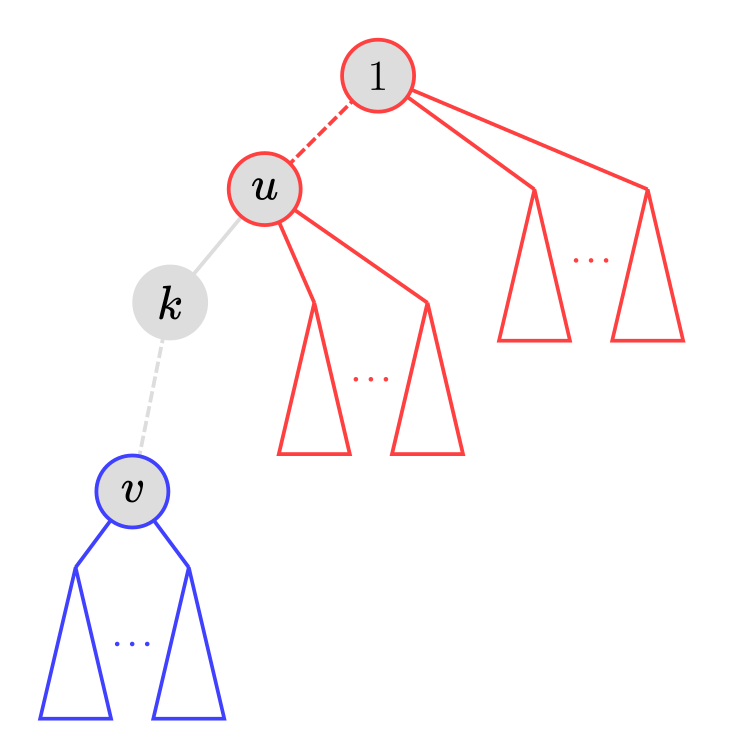
發現上面的方法沒有辦法直接用， 假設 $u$ 是 $v$ 的某一輩祖先， 可能的狀況是 $\{u$ 沒有 $v$ 的那些子樹與 $u$ 上面可以走到的所有點$\}$ 連接 $\{ v$ 的子樹$\}$。

令 $k$ 是所有 $v$ 的祖先且為 $u$ 的小孩中最靠近 $u$ 的那個（也就是 $u$ 下面有 $v$ 的那棵子樹的根）， 所以可能的狀況可以變成 $\{$全部點 $-k$ 的子樹$\}$ 連接 $\{ v$ 的子樹$\}$。

然而上面的環長度不能直接求期望值， 但是可以在計算 DP 的時候，順便計算以 $u$ 當根的時候，全部點距離總和是多少， 令對 $p$ 而言新計算的這個 DP 值為 $dp'[p]$， 由於原本那棵子樹不變，可以得到答案就是：

$$ \begin{align*} & \frac{dp'[u] - dp[k] + dis[k]size[k]}{N - size[u]} + \frac{dp[v] - dis[y]size[y]}{size[v]} + dis[v] - dis[u] + 1 \\ = & \frac{dp'[u] - dp[k] + dis[k]size[k]}{N - size[u]} + \frac{dp[v]}{size[v]} - dis[u] + 1 \end{align*} $$

求 $k$ 可以用倍增法得到，甚至可以跟 Case 1 共用一個函式。

AC Code

Link
終於把 Code 寫好看一點了 owo