[資料結構] 掃描線
TIOJ 1224, CF 524E, CF 833B, TIOJ 1872
先備知識
- 線段樹
基本上掃描線可以算是線段樹的一種變化,大部分的掃描線題都離不開線段樹。
經典題 - 矩形覆蓋面積計算
Link - TIOJ 1224
給你$N$個矩形,四邊範圍 $0 \leq L,\ R,\ D,\ U \leq 10^6$,
問你總覆蓋面積(重疊的只算一次)是多少。
做法
直接扣掉重疊面積好像有點難,
又不太容易套二維資料結構$^*$,
不如把每次覆蓋區域不一樣的地方都切成一條長條型,
這樣要計算的東西就是 $覆蓋量 \times 高度$,
不過要怎麼維護覆蓋量?
$*_{\scriptstyle 註:還是可行的,但是複雜度是O(N\log^2N)}$
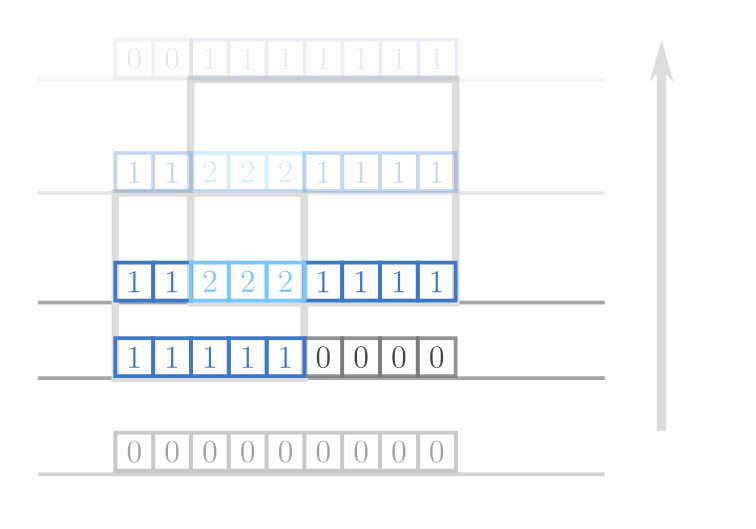
參考上面這張圖,當我加入一個矩形的時候,
必須要對區間都加一次值(代表多被覆蓋一次),
同樣,當一個矩形被掃完的時候,
必須要對區間都扣一次值(代表少被覆蓋一次),
但是每次我想知道的是有多少非$\,0\,$的值(代表覆蓋到的實際面積),
這樣就把原本的問題換成了區間操作的問題。
實作上可以使用線段樹,
由於在線段樹上一個區間可以被拆成$\log N$個區間,
所以在每個區間的值就是
- 如果被蓋到,就是整個區間的長度
- 否則,回傳兩個子區間相加
這樣,總複雜度$\mathcal O(N \log N)$。
基本概念差不多只有這樣,
不過要做到更好,可以對區間做離散化,
做起來會跟一般線段樹不太一樣,但基本上都是對區間做出修改。
Code
#include <bits/stdc++.h>
#define ll long long
#define pii pair<int, int>
#define F first
#define S second
#define pb(x) emplace_back(x)
#define fast ios::sync_with_stdio(0), cin.tie(0)
using namespace std;
int n, m, seg[400000], lazy[400000];
ll ans;
vector<int> t;
vector<int> pos;
vector<pair<int, pii>> add;
vector<pair<int, pii>> rem;
void push(int l, int r, int i)
{
if (lazy[i] > 0)
{
lazy[i * 2] += lazy[i];
lazy[i * 2 + 1] += lazy[i];
lazy[i] = 0;
seg[i] = (pos[r] - pos[l]);
}
}
void pull(int l, int r, int i)
{
int mid = (l + r) / 2;
if (lazy[i] > 0)
seg[i] = (pos[r] - pos[l]);
else
seg[i] = (lazy[i * 2] > 0 ? (pos[mid] - pos[l]) : seg[i * 2]) +
(lazy[i * 2 + 1] > 0 ? (pos[r] - pos[mid]) : seg[i * 2 + 1]);
}
void modify(int l, int r, int i, int a, int b, int val)
{
if (l == r)
return;
if (b <= l || r <= a)
return;
if (a <= l && r <= b)
lazy[i] += val;
else
{
int mid = (l + r) / 2;
modify(l, mid, i * 2, a, b, val);
modify(mid, r, i * 2 + 1, a, b, val);
}
pull(l, r, i);
}
signed main()
{
fast;
int n;
cin >> n;
for (int i = 1; i <= n; i++)
{
int l, r, d, u;
cin >> l >> r >> d >> u;
t.pb(d);
t.pb(u);
pos.pb(l);
pos.pb(r);
add.pb(make_pair(d, pii{l, r}));
rem.pb(make_pair(u, pii{l, r}));
}
t.pb(-1);
sort(t.begin(), t.end());
t.resize(unique(t.begin(), t.end()) - t.begin());
sort(pos.begin(), pos.end());
pos.resize(unique(pos.begin(), pos.end()) - pos.begin());
sort(add.begin(), add.end(), greater<pair<int, pii>>());
sort(rem.begin(), rem.end(), greater<pair<int, pii>>());
for (int i = 1; i < t.size(); i++)
{
pull(0, pos.size() - 1, 1);
ans += (ll)(t[i] - t[i - 1]) * seg[1];
while (!add.empty() && add.back().F == t[i])
{
int L = lower_bound(pos.begin(), pos.end(), add.back().S.F) - pos.begin(),
R = lower_bound(pos.begin(), pos.end(), add.back().S.S) - pos.begin();
modify(0, pos.size() - 1, 1, L, R, 1);
add.pop_back();
}
while (!rem.empty() && rem.back().F == t[i])
{
int L = lower_bound(pos.begin(), pos.end(), rem.back().S.F) - pos.begin(),
R = lower_bound(pos.begin(), pos.end(), rem.back().S.S) - pos.begin();
modify(0, pos.size() - 1, 1, L, R, -1);
rem.pop_back();
}
}
cout << ans << '\n';
}
整理
剛剛我們做了什麼事讓原本$\mathcal O(N^2)$的事降到$\mathcal O(N \log N)$?
一個很重要的關鍵是,對於原本的問題,
本來要按照輸入順序做的東西,把他按照順序排好之後,
用時間掃過一個維度(或是一項要維護的問題),
然後其他按照順序去做處理。
接下來有很多掃描線的問題可能題目並沒有一個圖,
但實際觀點有點像在平面上維護一些性質。
例題 - Codeforces 524E Rooks and Rectangles
Link
給你一個 $N \times M$ 的矩形,上面有 $K$ 個城堡(可以走直或橫),
$Q$次詢問一個矩形是不是每格都被矩形內的城堡保護到。
$N,\ M \leq 10^5$
$K,\ Q \leq 2 \times 10^5$
觀察
一個矩形要被完全保護到,一定滿足:
- 直的每一列上都要有城堡
- 否則橫的每一行都要有城堡
所以問題就簡單一點了,問題是單獨查詢每一列複雜度是可怕的$\mathcal O(QN\log N)$。
做法
首先,有了剛才的觀察,就只要先討論一個方向就好,
另一個方向可以用一樣的方法解決。
看到二維的東西,然而又不能用二維的資料結構處理,
所以轉向去思考:有沒有可能用時間慢慢掃過一維處理?
想像一條掃描線從左掃到右,記錄當下的狀況,
但是遇到的問題是:查詢不僅是在線上的一個區間,還有時效的限制。
剛剛想到用時間處理一維,但是掃描線只解決了右界的問題,
那左界呢?可以想成過期的條件,
也就是說我可以查看看最好的解,再回來用左界看看他是不是過期了,
如果這個最好的解過期了,表示其他所有解都一定過期了。
換句話說,
當我掃到一個查詢的右界的時候,在當下就回答那個查詢,
並且對所有左界都可以處理那個查詢。
實作
既然我們有把「左界當成過期」的想法,那要怎麼知道有沒有過期?
剛剛有提到,「先查看看最好的解,再看看他有沒有過期」,
所以對於每一橫排,當我掃到$\,R\,$的時候,
需要把左邊所有的城堡都放進去,
也就是保留$\,R-1\,$的狀況,新增在$\,R\,$上的城堡,
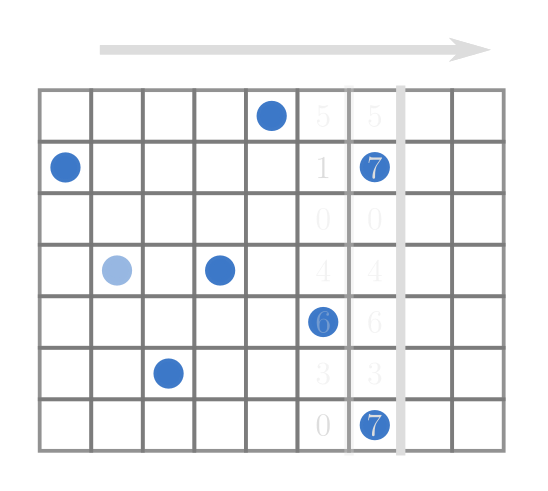
當我遇到那一橫排有新的加入,就覆蓋掉前面的,
因為當我回答的時候可以想像成從右界開始往左掃回去,所以越右邊的會越好。
查詢的時候只要看區間裡最早出現的元素(最小值),
再拿去跟左界比較有沒有過期。
時間複雜度$\mathcal O(Q \log Q + Q \ log N + K \log N )$。
Code
類題 - Codeforces 833B The Bakery
給你一個長度為$\,N\,$的陣列,要你剛好切成$\,K\,$塊,
其中每塊的價值是那一塊中相異元素的數量,問最大價值。
觀察
稍微想一下,可以設出DP狀態:
$dp[i][j]$ 表示已經安排好$[1..i]$的部分,而且已經切了$\,j\,$塊的最大價值。
問題是轉移時需要$\mathcal O(N)$,需要優化。
但是看一下DP計算的順序,剛好是 $1 \rightarrow N$ ,
這樣來看,似乎可以套用掃描線的技巧?
做法
如果我需要用線段樹加速DP,就要想辦法維護轉移的價值,
這樣只要單點修改加上之前的DP值就可以在$\mathcal O(\log N)$的時間計算出來,
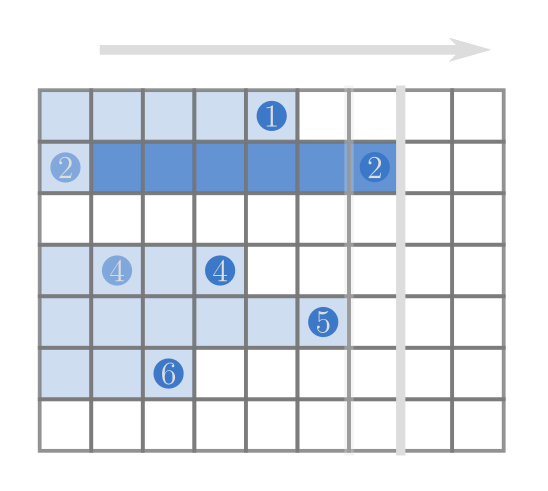
觀察到每個數字排在一行上,其實跟上一題的情況有點像,
只需要改一下維護的值,
當同樣一個數字出現的時候,需要對$[上次出現+1..這次出現]$加值,
類題 - TIOJ 1872 最小公倍數
Link - TIOJ 1872
給定一個長度為 $N$ 的陣列 $c$,$Q$ 次查詢區間最小公倍數$\mod 10^9 + 7$。
$N,\ Q,\ c_i \leq 10^6$。
觀察
區間中的LCM似乎沒有辦法好好的用兩個數字的LCM做,是一個最大的問題。
區間$[i, j]$要求的其實是$\displaystyle \prod_{p \in \mathbb{P}}p_k^{\max{a_k}}$。
但是直接對每個質數維護是不夠好的,複雜度為$\mathcal O(\displaystyle Q \frac{N}{\log N} \log N ) = \mathcal O(QN )$。
(質數個數$\mathcal O(\displaystyle\frac{N}{\log N})$)
做法
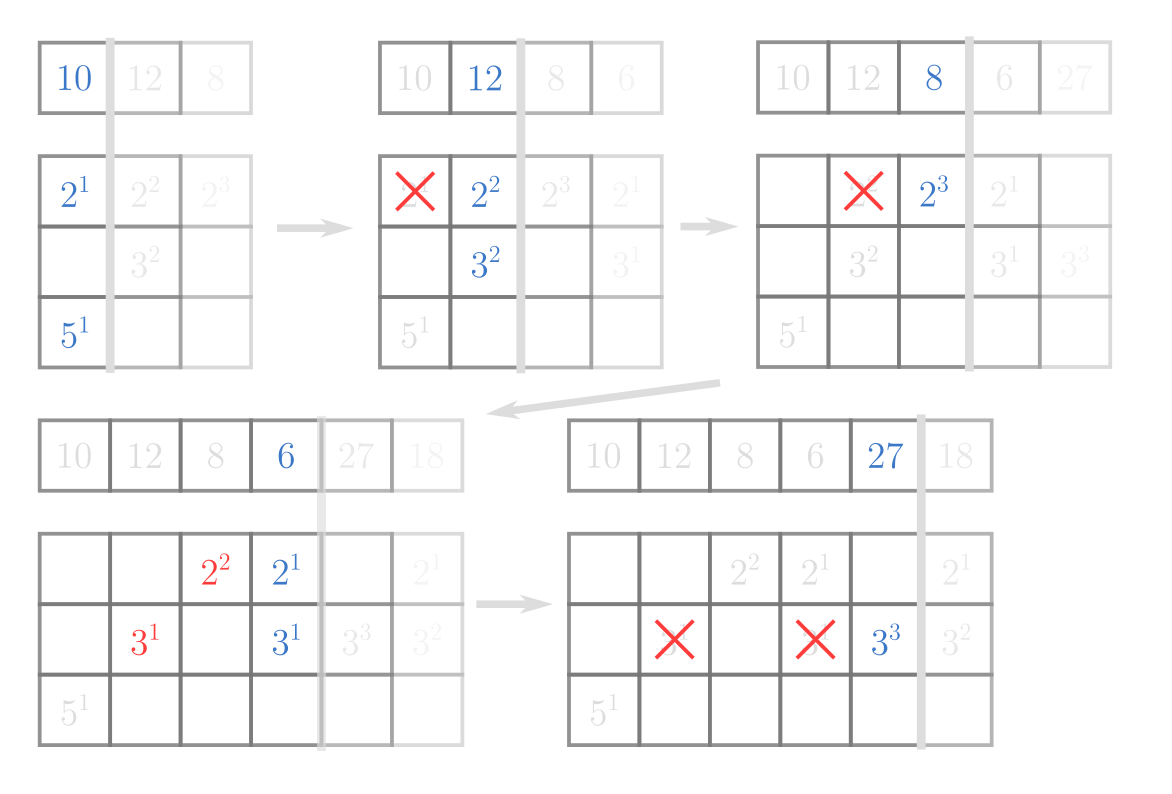
把質因數分解之後,一一對齊會長的像是:

還記得剛剛優化的核心概念嗎?
當我掃到一個查詢的右界的時候,在當下就回答那個查詢,
並且對所有左界都可以處理那個查詢。
也就是說,從右界往左的所有後綴區間都是有效的。
這裡我的做法用區間乘積維護答案,
對於每個質數都要有一個單調隊列依序遞減,
所以區間乘積就要透過差分去做拆解:
- 當新的次方較大,就把舊的刪除
- 否則,差分完丟進我們維護的線段樹內
如觀察所述,我需要做到:
- 質數篩 + DP $\mathcal O(C + \sqrt C \log \log C)$
- 質因數分解 $\mathcal O(\log C)$
- 按右界sort一次查詢$\mathcal O(Q \log Q)$
- 每次對 $\mathcal O(\dfrac{\log C}{\log \log C})$ 個質因數的單調隊列更新 均攤$\mathcal O(1)$
- 每次單調隊列更新就更新線段樹 $\mathcal O(\log N)$
- 回答查詢$\mathcal O(Q\log N)$
總複雜度$\mathcal O(C + Q\log Q + Q \log N + \dfrac{ N \log N \log C}{\log \log C} + N \log C)$。
Code
/* | | _ _ | | _____ | |
// | | _ | | | | | | _____ / ___|__ __| |___ _____
// | | |_|[ ][ ]| |/ _ \| | | | | | _ \/ _ \
// | L__| | | |_ | |_| || ____|| |___ | |_| | |_| || ____|
// L____|_| |___||___|_|\_____|\_____|\_____/\____/\_____|
// Segment Tree is hard.
*/
#pragma GCC optimize("Ofast,unroll-loops")
#include <bits/stdc++.h>
#pragma pack(0)
#define ll long long
#define pii pair<int, int>
#define pll pair<ll, ll>
#define F first
#define S second
#define MOD 1000000007
#define fast ios::sync_with_stdio(0), cin.tie(0)
using namespace std;
struct Q
{
ll i, l, r;
};
ll n, q, arr[1000005], sieve[1000005], seg[4000000], prime[1000005], idx = 1, ans[1000005];
vector<pii> mq[1000000];
vector<Q> query;
ll fastpow(ll base, ll p)
{
ll a = 1, b = base;
while (p > 0)
{
if (p & 1)
a = a * b % MOD;
b = b * b % MOD;
p >>= 1;
}
return a;
}
void Modify(int l, int r, int i, int pos, ll val)
{
seg[i] = seg[i] * val % MOD;
if (l == r)
return;
int mid = (l + r) / 2;
if (pos <= mid)
Modify(l, mid, i * 2, pos, val);
else
Modify(mid + 1, r, i * 2 + 1, pos, val);
}
ll Query(int l, int r, int i, int a, int b)
{
if (a <= l && r <= b)
return seg[i];
else if (b < l || r < a)
return 1;
else
{
int mid = (l + r) / 2;
return Query(l, mid, i * 2, a, b) * Query(mid + 1, r, i * 2 + 1, a, b) % MOD;
}
}
signed main()
{
fast;
for (int i = 2; i <= 1000000; i += 2)
sieve[i] = 2;
prime[2] = 1;
for (int i = 3; i <= 1000000; i += 2)
if (sieve[i] == 0)
{
sieve[i] = i;
prime[i] = ++idx;
for (int j = i * i; j <= 1000000; j += i)
sieve[j] = i;
}
cin >> n >> q;
for (int i = 1; i <= n; i++)
cin >> arr[i];
for (int i = 1; i <= q; i++)
{
int l, r;
cin >> l >> r;
query.emplace_back(Q{i, l, r});
}
for (int i = 1; i < 4000000; i++)
seg[i] = 1;
sort(query.begin(), query.end(), [](Q q1, Q q2) { return q1.r < q2.r; });
idx = 0;
for (int i = 1; i <= n; i++)
{
while (arr[i] > 1)
{
ll base = sieve[arr[i]], p = 0;
while (arr[i] % base == 0)
arr[i] /= base, p++;
while (!mq[prime[base]].empty() && p >= mq[prime[base]].back().S)
{
pii last = mq[prime[base]].back();
Modify(1, 1000000, 1, last.F, fastpow(base, last.S * (MOD - 2) % (MOD - 1)));
mq[prime[base]].pop_back();
if (!mq[prime[base]].empty())
Modify(1, 1000000, 1, mq[prime[base]].back().F, fastpow(base, last.S));
}
ll res = fastpow(base, p);
Modify(1, 1000000, 1, i, res);
if (!mq[prime[base]].empty())
Modify(1, 1000000, 1, mq[prime[base]].back().F, fastpow(res, MOD - 2));
mq[prime[base]].emplace_back(make_pair(i, p));
}
while (idx < q && query[idx].r == i)
{
ans[query[idx].i] = Query(1, 1000000, 1, query[idx].l, query[idx].r);
idx++;
}
if (idx > q - 1)
break;
}
for (int i = 1; i <= q; i++)
cout << ans[i] << '\n';
}
離線限制?
剛剛所有提到的做法都要剛剛好是離線sort的狀態,
那有沒有可以在線回答的方法呢?
答案是有,只要有效率地把所有東西都存下來就可以,
如果以線段樹作為儲存資料結構,
那只要把它持久化就可以做到在線詢問了。