[數論] 質數與模運算
[2/7] 從寒訓整理一些東西出來
不然我好像會跟不上:(
[6/2] 重新翻修,發現以前寫錯好多;w;
[7/29] 更新一些小細節
[8/16] 修正一些小錯誤與排版
質數篩法
最基礎的想法
用一個陣列維護當前的質因數個數,最容易想也做容易寫,
實作上從 3 開始判奇數及質數用到 $\sqrt{N}$ 就停止可以節省一些常數。
原因是因為如果某數 $N$ 存在大於 $\sqrt{N}$ 的質因數 $d$,$\dfrac{\displaystyle N}{\displaystyle d}$ 也是 $N$ 的一個因數且 $\dfrac{\displaystyle N}{\displaystyle d} < \sqrt{N}$,
對於 $N$ 個數字,有 $\dfrac{1}{2}$ 是在第 $1$ 步被篩到,$\dfrac{1}{6}$ 在第 $2$ 步被篩到,$\dfrac{1}{15}$ 在第 $3$ 步被篩到,以此類推,
而 $N$ 以下大約會有 $\dfrac{N}{\log N}$ 個質數,
估計這個數列,可以發現他有以下的遞迴式:
$S_n = \dfrac{\prod_{i = 1}^{n - 1} p_i \cdot n}{\prod_{i = 1}^{n} p_i} + S_{n - 1}$
粗略估計一下,總和應該是 $\mathcal{O}(N)$ 的,而剩下的質數所需要的時間會比較長,
複雜度大概是 $\mathcal{O}(\dfrac{N \sqrt N}{\log N})$。
Code
#include <bits/stdc++.h>
using namespace std;
int prime[100000], index = 1;
int main()
{
//Easy Sieve
// | Range | Time |
// |-------|--------|
// | 1e5 | 3 ms |
// | 1e6 | 76 ms |
// | 1e7 | 1.5 s |
prime[0] = 2;
for (int i = 3; i < 1000000; i += 2)
{
bool isprime = true;
for (int j = 0; prime[j] <= sqrt(i) && isprime; j++)
if (!(i % prime[j]))
isprime = false;
if (isprime)
prime[index++] = i;
}
}
埃式篩法
基本上跟上個做法很像,不過換成:
如果找到一個質數,把這個質數的所有倍數都標記為不是質數,
這個算法的優化也跟上一個差不多。
對於 $N$ 個數字,有 $\dfrac{\displaystyle1}{\displaystyle2}$ 被 $2$ 篩到,$\dfrac{\displaystyle1}{\displaystyle3}$ 被 $3$ 篩到,最後的數列接近:
$N \times (\dfrac{\displaystyle1}{\displaystyle2} + \dfrac{\displaystyle1}{\displaystyle3} + \dfrac{\displaystyle1}{\displaystyle5} + \dfrac{\displaystyle1}{\displaystyle7} + \cdots) = N \ln \ln N$
優化後的複雜度約為 $\mathcal{O}(N \log \log N)$
實作上程式較短,也比較容易優化,
Code
#include <bits/stdc++.h>
using namespace std;
bitset<100000> notprime = 3;
int main()
{
//Eratosthenes Sieve
// | Range | Time |
// |-------|--------|
// | 1e5 | 1 ms |
// | 1e6 | 12 ms |
// | 1e7 | 144 ms |
// | 4e7 | 630 ms |
// | 5e7 | 833 ms |
// | 1e8 | 1.9 s |
//Pre-compute all 2n except 2
for (int i = 4; i < 100000; i += 2)
notprime[i] = 1;
//Main Program
for (int i = 3; i < sqrt(100000); i += 2)
if (!notprime[i])
for (int j = i * 3; j < 100000; j += i * 2)
notprime[j] = 1;
}
線性篩法
線性篩法的精神是
如果有一個數是合數,那他就應該只被篩掉一次,
如果某個數字 $K = p_1 p_2 p_3 \cdots p_n$,其中 $p_1 \leq p_2 \leq p_3 \leq \cdots \leq p_n$,
我們希望他只被最大的東西篩掉,所以排除自己,最大的就是 $p_2 p_3 \cdots p_n$,
對於每個數 $C = p_1 p_2 p_3 \cdots p_n$,可以篩掉 $p \times p_1 p_2 p_3 \cdots p_n$,
其中 $p \leq p_1$,否則我們篩掉的那個數字有更大的合數因數:$p p_2 p_3 \cdots p_n$。
複雜度是 $\mathcal{O}(N)$,由於每個數都只會被篩到一次(或不被篩到)。
Code
#include <bits/stdc++.h>
#define N 20000000
using namespace std;
bitset<N + 1> notprime = 3;
vector<int> prime;
int main()
{
//Linear Sieve
// | Range | Time |
// |-------|--------|
// | 1e5 | 3 ms |
// | 1e6 | 36 ms |
// | 1e7 | 362 ms |
// | 2e7 | 732 ms |
// | 1e8 | 3.8 s |
for (int i = 2; i <= N; i++)
{
if (!notprime[i])
prime.emplace_back(i);
for (auto j : prime)
{
if (i * j > N)
break;
notprime[i * j] = 1;
if (!(i % j))
break;
}
}
}
質數篩法+DP
如果在篩掉的時候順便紀錄是被誰篩掉的,可以在短時間求得質因數相關問題的解,
如果要遞迴下去做也可以快速的知道其中的兩個因數。
這樣可以做到 $\mathcal{O}(\log C)$ 質因數分解,對於一些問題是很好用的。
更快的方法
當然有,不過這裡先不多做講解。
GCD
貝祖定理
若 $a,b,c \in \mathbb{Z}^{+}$,則有
$ax+by=c$ 存在整數解 $x = x_0,\,y = y_0\;\Leftrightarrow\; gcd(a,b)|c$
證明:
-
$(\Rightarrow)$
若 $ax+by=c$ 存在整數解 $x = x_0,\,y = y_0$,
則 $ax_0+by_0=c$
由於 $gcd(a,b)|a, gcd(a,b)|b$,
故原式可寫為 $gcd(a,b)(\dfrac{\displaystyle a}{\displaystyle gcd(a,b)}x_0+\dfrac{\displaystyle b}{\displaystyle gcd(a,b)}y_0)=c$
故 $gcd(a,b)|c$,得證 -
$(\Leftarrow)$
-
Lemma 1: $\exists s,t \in \mathbb{Z}$ 使得 $as+bt = gcd(a,b)$
證明:
由於 $gcd(a,b) > 0$
所以假設集合 $S = \{ax + by > 0 |x , y \in \mathbb{Z}\}$(所有正的$a$跟$b$的線性組合)
$\text{W.L.O.G.}$ 假設 $a < b$,所以 $b - a > 0$,
集合$S$非空(至少有一個元素 $b - a$)根據良序定理(Well-ordering theorem),存在一個最小的 $d = ax' + by'$
再根據除法定理,存在 $q,\,r$ 同時滿足 $0 \leq r < ax' + by' = d$ 且 $a = qd + r$發現到$r = a - qd = a - q(ax' + by') = a(1 - qx') + bqy'$(即$r$也是$a$跟$b$的線性組合)
又由前面的假設,$0 \leq r < d$,
所以得到 $r = 0$。否則$S$內最小元素應該是$r$而不是$d$,矛盾。
也就是說 $a = qd + r = qd$,$d|a$,同理可證$d|b$,所以$d$是$a,\, b$的一個公因數。
所以 $d|gcd(a,b)$,
而$ax + by = d$有解,所以$ax + by = gcd(a,b)$也有解。
由上面的引理,因為$gcd(a,b)|c$,
$ax + by = gcd(a,b)$有解,所以$ax + by = c$也有解。 -
擴展歐幾里得算法
如果原式 $ax+by=c$ 有解,可以轉換為:
$bx + (a \mod b)y = c$ 有解(由於這樣處理GCD不變,仍然有解)
接下來要想辦法讓他跟原式產生關係:
$\begin{align*}
bx' + (a \mod b)y' & = c \newline
bx' + (a - b\Big\lfloor\dfrac{\displaystyle a}{\displaystyle b}\Big\rfloor)y' & = c \newline
bx' + ay' - b\Big\lfloor\dfrac{\displaystyle a}{\displaystyle b}\Big\rfloor y' & = c \newline
ay' + b(x' - \Big\lfloor\dfrac{\displaystyle a}{\displaystyle b}\Big\rfloor y') & = c \newline
\end{align*}$
所以可以透過遞迴的方式把問題縮小,
中間 $a,\,b$ 其實就是做GCD的過程,必會遇到其中一項為 $0$ 的情況,可以直接解出來。
求出來的答案有個 bound,這部分等我想到再補。
注意對於負數要特判,先取絕對值,計算出來再把符號加回去。
Code
#include <bits/stdc++.h>
using namespace std;
// Notice the sign of a, b
void exgcd(int a, int b, int c, int &x, int &y)
{
if (b == 0)
x = c / a, y = 0;
else
{
exgcd(b, a % b, c, y, x);
y -= x * (a / b);
}
}
模運算
如果有兩個數字 $a,\,b$ 除 $m$的餘數相等,即 $m|(a-b)$ ($m$ 整除 $a-b$)
記為 $a \equiv b \mod m$。
基本運算
- $a \equiv b \mod m,\, c \equiv d \mod m \Rightarrow a+c \equiv b+d \mod m$ (同mod下同加)
- $a \equiv b \mod m,\, c \equiv d \mod m \Rightarrow ac \equiv bd \mod m$ (同mod下同乘)
- $a \equiv b \mod m,\, \Rightarrow a^k \equiv b^k \mod m$ (同mod下同次方)
證明:$m|(a-b) \Rightarrow m|(a-b)(a^{k-1} + a^{k-2}b^1 + a^{k-3}b^2 + \cdots + b^{k-1}) \Rightarrow m|(a^k-b^k)$ - $ca \equiv cb \mod n \Rightarrow a \equiv b \mod \dfrac{\displaystyle n}{\displaystyle gcd(n, c)}$
證明:令$d = gcd(n, c)$
$n|c(a-b) \Rightarrow \dfrac{\displaystyle n}{\displaystyle d}|\dfrac{\displaystyle c}{\displaystyle d}(a-b)$
而且 $gcd(\dfrac{\displaystyle n}{\displaystyle d}, \dfrac{\displaystyle c}{\displaystyle d}) = 1$
故 $\dfrac{\displaystyle n}{\displaystyle d}|(a-b)$
$\Rightarrow a \equiv b \mod \dfrac{\displaystyle n}{\displaystyle d}$
剩餘系
定義:
-
完全剩餘系:對某個集合裡的數$\mod m$之後,恰有$m$個相異的數字
-
非負最小完全剩餘系:對$\mod m$下,非負最小完全剩餘系為$\{ 0,1,\cdots,m-1 \}$
-
簡化剩餘系:任意一個完全剩餘系只保留與$m$互質的數
-
非負最小簡化剩餘系:非負最小完全剩餘系只保留與$m$互質的數\
例如考慮$\mod 6$下
完全剩餘系可以是$\{6, -5, -10, 603, 10, 17\}, \{0, 1, 2, -3, -2, -1\} \cdots$
但非負最小完全剩餘系只能是$\{0,1,2,3,4,5\}$
非負最小簡化剩餘系也只能是$\{0,5\}$
有限體
根據模運算的規則,我們可以定義一種代數結構(稱為體):
對於$n > 1$,定義$\langle \mathbb{Z}_n, +_n, \times_n \rangle$(簡寫為$\mathbb{Z}_n$)
其中:
$\mathbb{Z}_n = \{ 0,1,\cdots,m-1 \}$
$ \forall a, b \mod n \in \mathbb{Z}_n
\begin{cases}
a +_n b := (a + b) \mod n \newline
a \times_n b := (a \times b) \mod n
\end{cases} $
其實就是程式中的 % 運算(在非負數下),
而且 $\mathbb{Z}_n$ 同時滿足:
-
$ \begin{cases} (a +_n b) +_n c = a +_n (b +_n c) \newline (a \times_n b) \times_n c = a \times_n (b \times_n c) \end{cases} \newline$ (結合律)
-
$ \begin{cases} a +_n b = b +_n a \newline a \times_n b = b \times_n a \end{cases} \newline$ (交換律)
-
$ (a +_n b) \times_n c = a \times_n c +_n b \times_n c$ (分配律)
模逆元及反元素
如果存在兩個數$a, b \in \mathbb{Z}_n$滿足$a \times_n b = 1$,
我們稱 $b$ 是 $a$ 的反元素,記為 $a^{-1}$
$a \times_n b = 1 \Leftrightarrow b := a^{-1}$
在$\mod m$ 下也有這樣的定義,稱為模逆元:
$ab \equiv 1 \mod m \Leftrightarrow b \equiv a^{-1} \mod m$
在$\mathbb{Z}_n$(或$\mod n$下),不是每個元素都有反元素(模逆元),
例如$\mathbb{Z}_9$下:
| $a$ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| $a^{-1}$ | 無 | 1 | 5 | 無 | 7 | 2 | 無 | 4 | 8 |
由於模逆元可以用擴展歐幾里得算法求出來,
例如 $a$ 在$\mod m$ 下的模逆元可以用
$aa^{-1} + bm = 1$,此時 $gcd(a, m)$ 只能為 $1$,即兩數互質
如果需要建反元素\模逆元表,可以用以下推導出的遞迴式:
$\begin{align*}
P - i \times \left\lfloor\dfrac{\displaystyle P}{\displaystyle i}\right\rfloor & = P \% i \newline
P - i \times \left\lfloor\dfrac{\displaystyle P}{\displaystyle i}\right\rfloor & \equiv P \% i \mod P \newline
P \times i - i \times \left\lfloor\dfrac{\displaystyle P}{\displaystyle i}\right\rfloor & \equiv P \% i \mod P \newline
i \times (P - \left\lfloor\dfrac{\displaystyle P}{\displaystyle i}\right\rfloor) & \equiv P \% i \mod P \newline
i \times (P - \left\lfloor\dfrac{\displaystyle P}{\displaystyle i}\right\rfloor) (P \% i)^{-1} & \equiv 1 \mod P \newline
(P - \left\lfloor\dfrac{\displaystyle P}{\displaystyle i}\right\rfloor) (P \% i)^{-1} & \equiv i^{-1} \mod P \newline
i^{-1} & \equiv (P - \left\lfloor\dfrac{\displaystyle P}{\displaystyle i}\right\rfloor) (P \% i)^{-1} \mod P \newline
\end{align*}$
這樣就能夠在 $\mathcal{O}(P)$ 內建完反元素表了。
Code
Code
#include <bits/stdc++.h>
#define N 9
using namespace std;
int inv[N];
void build_inv()
{
inv[1] = 1;
for (int i = 2; i <= N; i++)
inv[i] = ((N - (N / i)) * inv[N % i]) % N;
}
費馬小定理
在$\mod p$下,對於任意整數$a$及質數$p$,有:
$a^{p} = a \mod p$
$a^{p-1} = 1 \mod p$
$a^{p-2} = a^{-1} \mod p$ (三個其實是同一式)
[證明]
對於$a, 2a, 3a, \cdots, (p-1)a$在$\mod p$下必須一一對應到$1, 2, 3, \cdots, p-1$,
否則兩個同樣餘數的相減就可以得到$a|p$的矛盾,
連乘之後得到
$(p-1)!a^{p-1} \equiv a \times 2a \times \cdots \times (p-1)a \equiv 1 \times 2 \times \cdots \times (p-1) \equiv (p-1)! \mod m$
$a^{p-1} \equiv 1 \mod m$,得證
所以反元素有另一種求法是透過費馬小定理,前提是$m$是質數,
此時$a^{-1} = a^{p-2} \mod p$
歐拉函數
定義
歐拉函數$\Phi(n)$的值表示在$1, 2,…,n$中與$n$互質的個數
常用$\mathbb{Z}_n^{*}$代表從$\mathbb{Z}_n$中與$n$互質的數,也就是說$\mathbb{Z}_n^{*}$有$\Phi(n)$個數
求值
求歐拉函數$\Phi(n)$的值,最暴力的方法是檢查每個$d$滿足$gcd(n, d) \neq 1$,
更快的方法是對於$gcd(m, n) = 1, \Phi(mn) = \Phi(m)\Phi(n)$
證明:
把$mn$個數排成下面的樣子:
$\begin{bmatrix}
1 & 2 & 3 & \cdots & m \newline
m + 1 & m + 2 & m + 3 & \cdots & 2m \newline
2m + 1 & 2m + 2 & 2m + 3 & \cdots & 3m \newline
\vdots & \vdots & \vdots & \ddots & \vdots \newline
(n-1)m + 1 & (n-1)m + 2 & (n-1)m + 3 & \cdots & nm
\end{bmatrix}$
每一橫列都有$\Phi(m)$個元素是跟$m$互質的,
而且$kp + r \equiv r \mod m$,所以有$\Phi(m)$個直排是與$m$互質的,
每一直排也都有 $\Phi(n)$ 個元素是跟 $n$ 互質的,
因為把每一直排都寫成 $km+r$ 的樣式,每一個必須在$\mod n$ 下一一對應到 $0, 1, …, n-1$
否則可以找到 $(k_0 - k_1)m|n$,也就是說兩數不互質的矛盾,
所以可以得到有 $\Phi(m)$ 個直排與 $m$ 互質,每排有 $\Phi(n)$ 個元素是跟 $n$ 互質,
因為與 $m,\,n$ 都互質的元素也會跟 $mn$ 互質,
(否則,它跟 $mn$ 的GCD一定也是 $m$ 或 $n$ 的因數)
得證 $gcd(m, n) = 1, \Phi(mn) = \Phi(m)\Phi(n)$
不過同時可以發現,如果可以把某個數換成質數的乘積,就可以把他們全部乘起來:
$N = {p_1}^{a_1}{p_2}^{a_2}{p_3}^{a_3} \cdots {p_n}^{a_n}$
$\Phi(N) = \Phi({p_1}^{a_1})\Phi({p_2}^{a_2})\Phi({p_3}^{a_3}) \cdots \Phi({p_n}^{a_n})$
如果某數 $M$ 是某個質數 $p$ 的 $k$ 次方,與他不互質的數必定是 $p$ 的倍數,共有 $\dfrac{\displaystyle M}{\displaystyle p}$ 個,故:
$\Phi(M) = M - \dfrac{\displaystyle M}{\displaystyle p} = M \times \dfrac{\displaystyle p-1}{\displaystyle p}$
套在前面的式子可以發現:
$\begin{align*}\Phi(N) & = {p_1}^{a_1} \cdot \dfrac{\displaystyle p_1-1}{\displaystyle p_1} \times
{p_2}^{a_2} \cdot \dfrac{\displaystyle p_2-1}{\displaystyle p_2} \times
{p_3}^{a_3} \cdot \dfrac{\displaystyle p_3-1}{\displaystyle p_3} \times
\cdots \times
{p_n}^{a_n} \cdot \dfrac{\displaystyle p_n-1}{\displaystyle p_n} \newline
& = N \displaystyle\prod \dfrac{\displaystyle p-1}{\displaystyle p}\end{align*}$
如果要同時求很多數字的歐拉函數,也可以用質數篩去蓋出來。
中國剩餘定理
定理
方程組
$ \begin{cases}
x \equiv a_1 \mod n_1 \newline
x \equiv a_2 \mod n_2 \newline
x \equiv a_3 \mod n_3 \newline
\vdots \newline
x \equiv a_k \mod n_k
\end{cases}$
當所有$1 \leq i,\, j \leq k,\; i \neq j$,都有 $n_i, n_j$ 互質時,$x$ 有解,
而且對於 $x' \equiv x \mod n_1n_2\cdots n_k$,$x'$ 也是一組解。
求解
如果方程組只有兩個式子:
$ \begin{cases}
x \equiv a_1 \mod n_1 \newline
x \equiv a_2 \mod n_2
\end{cases}$
可以化為:
$ \begin{cases}
x = pn_1 + a_1 \newline
x = qn_2 + a_2 \newline
\end{cases}$
$pn_1 + a_1 = qn_2 + a_2$
$pn_1 - qn_2 = a_2 - a_1$
由於$gcd(n_1 - n_2) = 1$,所以方程式必有解(而且不只一組),
利用擴展歐幾里得算法解得的$p, q$回推$x$,
而此時所有$x + kn_1n_2$都是答案,
對於多組方程式的問題,就可以使用分治,
合併時再使用擴展歐幾里得算法,
另一種想法是對於每個式子,都構建一個解$e_i$使得在$\mod n_i$下為$1$,其他為$0$,
這樣只要把$a_i e_i$加起來就是要求的$x$,
設$N = n_1n_2\cdots n_k$,$n_i^{*} = \dfrac{\displaystyle N}{\displaystyle n_i}$
顯然$e_i$為$n_i^{*}$的倍數,設$e_i = t_i n_i^{*}$,
現在要解的方程式就變為$t_i n_i^{*} \equiv 1 \mod n_i$,
把原本的方程式化為$t_i n_i^{*} + sn_i = 1$
就可以使用擴展歐幾里得算法找出解,
原本要解的$x$就變為$\sum_{n=1}^{k} a_i e_i$,
或是觀察這個式子$t_i n_i^{*} \equiv 1 \mod n_i$:
其實要求的$t_i$就是$\mod n_i$下的模逆元,
不過注意這邊不能直接一起合併為$1$,因為答案並不是在$\mod n_i$下,
所以要解的$x$就變為$\sum_{n=1}^{k} a_i t_i n_i^{*}$,
模逆元可以用遞迴方法求解,
總算法的時間複雜度是$\mathcal{O}(k \log \max\{n_i\})$
分治做法的 Code
#include <bits/stdc++.h>
using namespace std;
vector<int> a = {2, 3, 2}, n = {3, 5, 7};
void exgcd(int a, int b, int c, int &x, int &y)
{
if (b == 0)
x = c / a, y = 0;
else
{
exgcd(b, a % b, c, y, x);
y -= x * (a / b);
}
}
pair<int, int> solve(int L, int R)
{
if (L == R)
return make_pair(a[L], n[L]);
if (L + 1 == R)
{
int p, q, N = n[L] * n[R];
exgcd(n[L], n[R], a[R] - a[L], p, q);
return make_pair(((p * n[L] + a[L]) % N + N) % N, N);
}
pair<int, int> left = solve(L, (L + R) / 2), right = solve((L + R) / 2 + 1, R);
int p, q, N = left.second * right.second;
exgcd(left.second, right.second, right.first - left.first, p, q);
return make_pair(((p * left.second + left.first) % N + N) % N, N);
}
signed main()
{
cout << solve(0, 2).first;
}
擴展歐幾里得作法的 Code
#include <bits/stdc++.h>
using namespace std;
vector<int> a = {2, 3, 2}, n = {3, 5, 7};
void exgcd(int a, int b, int c, int &x, int &y)
{
if (b == 0)
x = c / a, y = 0;
else
{
exgcd(b, a % b, c, y, x);
y -= x * (a / b);
}
}
signed main()
{
int N = 1, ans = 0, t, s;
for (int i = 0; i < n.size(); i++)
N *= n[i];
for (int i = 0; i < n.size(); i++)
{
exgcd(N / n[i], n[i], 1, t, s);
ans = (ans + N / n[i] * a[i] * t) % N;
}
cout << ans;
}
組合計數
卡塔蘭數
卡塔蘭數有很多定義方法,常見的有這些:
- 長度為 $n$ 的合法括號字串
- $N \times N$ 的網格上,用右上-左下的主對角線隔開,走在右下那部分,只能往右以及往上,從左下走到右上不穿越主對角線的路徑數
- 長度為 $n$ 的 $\{1,\,-1\}$ 數列,任意前綴和非負的組合數
以下比較常考慮第二個計數方法,
定義 $C_0 = 1$,
由於任意 $N \geq 1$ 的時候,方法可以透過 向右 + ($i \times i$ 的方法) + 向上 + ($(n - i - 1) \times (n - i - 1)$ 的方法)構成,
所以有 $\displaystyle C_{n + 1}\sum_{i = 0}^{n} C_iC_{n - i}$ 的遞迴關係。
不過這樣計算 $C_n$ 需要 $O(n^2)$ 的時間,能不能更快?
觀察到每一個不合法的路徑都會通過主對角線而碰到上面的一條平行線,
但是把這條路徑對主對角線翻轉會出現太多一樣的路徑對應到同一種合法路徑,
所以考慮對上移一格的平行線做翻轉,
由於穿過主對角線表示目前往上多 $1$,而剩下的部分則是往右多 $1$,
因此翻轉後會是往上多 $2$,走到 $(n - 1,\, n + 1)$ 的位置,
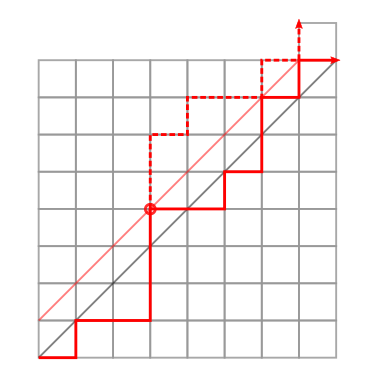
然後對於所有走到 $(n - 1,\, n + 1)$ 都會通過上移一格的對角線,
它們一一對應到一條不合法的路徑,而且不合法的路徑只有這些,
所以卡塔蘭數的一般式就是 $C_n = \binom{2n}{n} - \binom{2n}{n - 1} = \binom{2n}{n} - \dfrac{n}{n + 1}\binom{2n}{n} = \dfrac{1}{n + 1}\binom{2n}{n}$。
Reference
其他還有很多不同的意義以及一般式的證明方法,詳細參考:
Wikipedia - Catalan number