TOI 2023 二模
題目
A 區間統計 (interval)
[Batch, 3s/2 GB]
有 $n$ 個區間,開始與結束點 $a_i, b_i$ 都是 $1$ 到 $2n$ 中相異的整數點,且滿足開始點遞增($a_1 < a_2 < \cdots < a_n$)。
定義 $c_1(i), c_2(i), c_3(i), c_4(i)$ 表示對第 $i$ 個區間而言,包含 $[a_i, b_i]$、被 $[a_i, b_i]$ 包含、與 $[a_i, b_i]$ 互斥(交集為空)以及與 $[a_i, b_i]$ 部份重疊的其他區間數量。
給定 $c_1(i), c_2(i), c_3(i), c_4(i)$,請回溯出一組合法的 $a, b$。
- $2 \leq n \leq 3 \times 10^5$
- 對所有 $i$,$c_1(i) + c_2(i) + c_3(i) + c_4(i) = n - 1$
- 對所有輸入,保證存在一組合法的解
| 分數 | 額外輸入限制 |
|---|---|
| $7$ | $n \leq 7$ |
| $25$ | $c_4(i) = 0$ |
| $19$ | $n \leq 3000$ |
| $49$ | 無額外限制 |
B 圓周拉弦 (chord)
[Batch, 1s/2 GB]
有一個圓,上面有 $n$ 個等分點,連起兩個點 $i, j$ 所得到的分數是 $w_i + w_j \pmod k$,在連線只能交在端點的情況下,求最大分數。
- $3 \leq n \leq 500$
- $2 \leq k \leq 500$
- $0 \leq w_i \leq k$
| 分數 | 額外輸入限制 |
|---|---|
| $13$ | $n \leq 15$ |
| $24$ | $n \leq 100$ |
| $63$ | 無額外限制 |
C 磁磚整理 (tiles)
[Batch, 10s/2 GB]
本題有帶 grader 輸入及輸出。
有一個 $n \times n$ 的網格,每格是白(0)或黑(1),且對主對角線對稱,你想要把這個網格變成這個樣子:
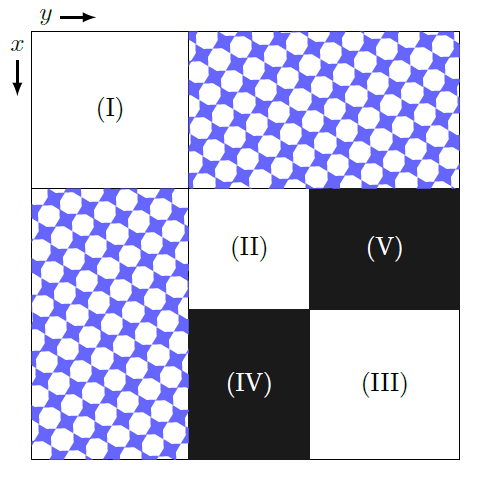
其中 $\text{I, II, III}$ 是全 0 的正方形,$\text{IV, V}$ 是全 1 的長方形,若長或寬是 $0$ 也算數(例如,全部都是白色也是一組解,因為 $\text I$ 的長寬是 $n$ 而其他的長寬都是 $0$)
你能做的操作是選擇兩個數字 $i, j$,把第 $i$ 行跟第 $j$ 行交換,再把第 $i$ 列跟第 $j$ 列交換,輸出有沒有一種操作序列可以使得網格長成上面的樣子,或決定不可能。
- $n \leq 10000$
- 輸出的操作序列長度不得超過 $20000$
| 分數 | 額外輸入限制 |
|---|---|
| $12$ | $n \leq 10$ |
| $40$ | $n \leq 500$ |
| $48$ | 無額外限制 |
D 餐桌邊緣 (table)
[Batch, 3s/2 GB]
空間中有一個平面 $x \in [-W, W], y \in [-L, L], z = 0$,平面的中心有個半徑為 $S$ 的球,球心在 $(0, 0, S)$,此外還有 $n$ 個圓柱與 $m$ 個圓錐,第 $i$ 個圓柱底面圓心在 $(x_i, y_i, 0)$,底面半徑是 $r_i$,高度是 $h_i$;第 $i$ 個圓錐底面圓心在 $(X_i, Y_i, 0)$,底面半徑是 $R_i$,高度是 $H_i$。
你想要把球滾到邊緣,也就是讓 $x = \pm W$ 或 $y = \pm L$,但過程中必須滿足:
- 球要接觸到桌面
- 球不能穿透桌面上的物體,但相切是可以的
- 圓柱跟圓錐不能移動
輸出最短距離,或決定不可能。輸出的絕對或相對誤差在 $10^{-6}$ 以內都視為正確。
- $1 \leq L, W, S \leq 10000$
- $0 \leq n, m \leq 100$
- $-W \leq x_i, X_i \leq W$
- $-L \leq y_i, Y_i \leq L$
- $1 \leq r_i, h_i, R_i, H_i \leq 1000$
- 輸入的所有物體中沒有兩個互相重疊
| 分數 | 額外輸入限制 |
|---|---|
| $10$ | $n \leq 2, m = 0$ |
| $11$ | $n = 0, m \leq 2$ |
| $20$ | $m = 0, h_i$ 全相同且 $> S$ |
| $22$ | $m = 0$ |
| $37$ | 無額外限制 |
比賽
讀完題發現 A 是什麼構造,B 是什麼 APCS 題就直接開寫了,
區間 DP 亂寫一下就做完了。
0:13 B 100
看完 C 是不知道什麼神仙的題目,一點都沒想法,D 感覺就是計算幾何詭譎最短路,所以先回去推 A
A 我想到的是第一個人的起點已經固定了,所以就能算他的終點然後把這個人拔掉,
所以我的過程中需要算第 $k$ 小的空格,想一下之後決定花時間去找 PBDS 的語法,
小技巧是我都這樣找:
cd /
find . | grep "extc++.h"
結果我好像是把 tree_order_statistics_node_update 打成 tree_order_statistic_node_update,怎麼會這樣…
寫完就過了,
0:51 A 100
接下來往 C 去開,我做一做毫無頭緒,把 grader 改了一下讓我可以手解之後,我(其實過了蠻久的時間)想到可以直接輸入
000222222
000222222
000222222
222000111
222000111
222000111
222111000
222111000
222111000
然後玩一玩發現等價找到一個集合 $S$ 使得 $S\times S$ 裡都是 1 然後把他們拔掉之後網格只有一種 mask 跟他的 inverse。
所以我就亂 claim 可以 greedy 找最大的 $S$,
2:22 C 0
我甚至不知道我為什麼會這樣想,因為根本就亂構都有反例阿,
修好變枚舉所有 $S$ 之後傳上去還是 WA,
2:30 C 0
另一個 bug 是我根本就沒構好解,
2:46 C 0
然後我把那個 bug 又修成 bug 了,改好之後就有分數了,
2:52 C 12
隨手再回去把那個 claim 弄回去,但顯然是不會有料,跟預期中一樣吃了一個 WA。
2:54 C 0
D 題把等價影響的範圍畫出來其實就是一個圓,而子題 3 其實就是不用算這件事,
接下來把原本的那個圓都擴張 $S$ 就變成一個點在圖上跑,考慮他跑的路徑是一條繩子,
這條繩子拉直之後會卡在一坨切線上,所以只要算所有切線跟圓射向上下左右的合法路徑,
再把圓上的點蒐集起來極角排序,把在其他圓裡面的點 ban 掉然後建邊就能跑最短路算答案了,
實際上實作有夠噁心的,我寫了 299 行連範測都錯,還有一個問題是就算只有兩三個圓建出來的東西也很大,
debug 難度極高,所以最後我亂傳亂修都還是沒有過。
4:50 C 0
4:53 C 0
4:54 C 0
Result
| A | B | C | D |
|---|---|---|---|
| 12 | 0 |
出場芒果用時間剪枝把 C 拿到 52、PixelCat 幾何巨男把 D 推到 21,好強,
我好像 A 在吃毒然後 C 沒看出來其實就是一個 Adjacency Matrix 然後交換兩個點的 label,
記分板出來二模大概就是一票的 212 跟 200,然後沒拿到 200+ 的人都虧爆了,
整場打得沒有很開心因為開場做掉 A、B 之後就是燒一題思維神仙題 C 跟一題實作神仙題 D,
比起一模來說沒有那麼好玩,
整體來說二模打得不算糟但也沒有打得很好,不過我沒打還是能進 2!
附件
題本跟範例互動程式:
2A.pdf
2B.pdf
2C.pdf
2C_sample.cpp
2C_sample_grader.cpp
2D.pdf